ENERGIA POTENCIAL ELECTRICA

Capitulo 3

Contenido: Energia Potencial Electrica y Potencial Electrico, Calculo de Potencial Electrico y Superficies Equipotenciales, Dipolo Electrico

Introduccion

Vamos a ver que es la energía potencial eléctrica, y después, ampliaremos su explicación física de forma detallada con ejemplos para que podamos entender el concepto fácilmente, incluso haciendo algunos ejercicios y explicando el potencial eléctrico, el campo eléctrico y su fórmula.

¿Qué es la Energía Potencial Eléctrica?

"La Energía Potencial Eléctrica es la energía que tiene una carga eléctrica debido a su posición en relación con otra u otras cargas eléctricas".

El movimiento de las cargas eléctricas es debido a esta energía.

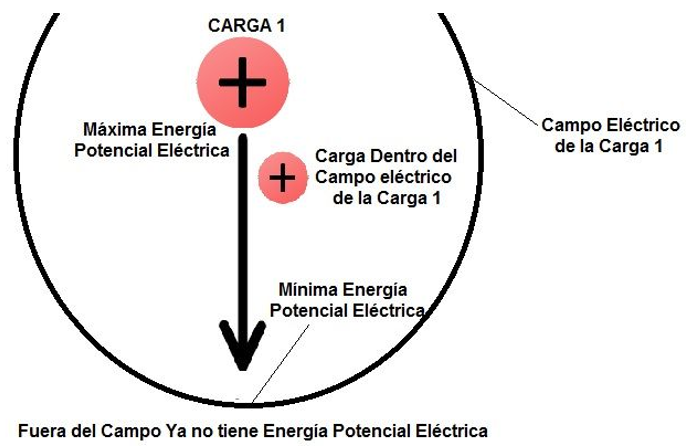
En la imagen anterior la carga pequeña tiene máxima energía potencial eléctrica cuando está pegada a la carga grande o carga 1, es por eso que si la soltamos se moverá por repulsión alejándose de la carga grande y perdiendo energía potencial eléctrica, pero ganando velocidad (energía cinética).

Las cargas eléctricas pueden tener carga positiva, por ejemplo un protón, o negativa, por ejemplo un electrón.

Las cargas eléctricas opuestas (positiva y negativa) se atraen, al igual que la Tierra atrae a una pelota. Las cargas iguales se repelen (por ejemplos dos cargas positivas o dos negativas).

Si tienes una pelota con la masa m y la elevas a cualquier altura, le estás dando (aumentando) energía potencial gravitatoria. Sabemos esto por dos razones: una, tienes que utilizar la energía de tus músculos para hacerlo, y dos, cuando se suelta la pelota, cae al suelo y la energía que tenía (potencial gravitatorio) se libera de nuevo, pero ahora en forma de energía cinética (velocidad). Aumenta su velocidad (su energía cinética) mientras va perdiendo energía potencial (altura).

La energía potencial eléctrica es similar, pero con cargas eléctricas en lugar de masas. En lugar de levantar una pelota dentro del campo gravitacional de la Tierra, una carga eléctrica se mueve cuando está en el campo eléctrico de otra carga. La pelota se mueve (cae) porque está dentro del campo gravitacional de la tierra,la carga eléctrica porque está dentro del campo eléctrico de otra carga.

Al separar o juntar dos cargas eléctricas una distancia (por ejemplo un radio r) dentro de sus campos eléctricos, le estas quitando o dando a las cargas eléctricas potencial energético, una respecto a la otra. Al soltar esas cargas, van a atraerse o repelerse, liberando esa energía eléctrica adquirida. Es similar también a dos imanes, pero los imanes será energía magnética.

Antes de comenzar con la explicación física paso a paso, donde explicaremos que es un campo eléctrico, la energía potencial eléctrica, su fórmula y el potencial eléctrico con cargas concretas, es bueno que recordemos los conceptos de energía y energía potencial.

La energía es la capacidad que tiene un cuerpo de realizar cambios o trabajo. Por ejemplo, en un velero el aire mueve el velero golpeando las velas. Luego el aire tiene energía por que es capaz de realizar cambios a su alrededor. Esos cambios que realiza se llaman Trabajo. El aire se convierte en movimiento del velero por lo tanto la energía del aire se ha transformado en energía de movimiento, el aire pierde su energía y la cede al velero. Ese cambio es lo que significa que la energía ni se crea ni se destruye, solo se transforma. El aire realiza trabajo cuando mueve el velero.

La energía potencial es la que poseen los cuerpos por estar en una determinada posición. La energía potencial más famosa es la energía potencial gravitatoria, es la energía que poseen los cuerpo por estar a una determinada altura. La gravedad de la tierra hace una fuerza sobre todos los cuerpos que están situados sobre ella, "Tira" de los cuerpo hacia abajo, por eso una piedra que esté a 10m de altura, si la soltamos la fuerza de gravedad tira de ella hasta que llega al suelo. Luego la piedra a 10m tiene una energía, esta energía se transformará en trabajo cuando la soltemos, ya que se moverá hasta llegar al suelo. Este trabajo se produce cuando la fuerza de la gravedad actúa sobre la piedra y la mueve una distancia, recuerda Trabajo = Fuerza x distancia. Cuando está quieta a una altura solo tiene energía, capacidad de realizar trabajo, pero no realiza ningún trabajo.

Bueno, pues cuando la piedra esta quieta, sin moverse a una cierta altura, tiene una energía, y como esta energía depende de la posición de la piedra (a más altura mayor energía) resulta que la piedra posee una energía potencial, energía potencial gravitatoria, por que es producida por la gravedad. ¿Lo tenemos claro? Pues ahora pasemos a explicar la energía potencial gravitatoria.

Energía Potencial Eléctrica

Los cuerpos que poseen carga eléctrica pueden tener carga positiva o negativa, por ejemplo un electrón tiene carga eléctrica negativa y un protón positiva.

Resulta que cuando un cuerpo tiene carga eléctrica genera una región de espacio a su alrededor (campo eléctrico) donde si introducimos otra carga eléctrica, esta se verá afectada por la primera.

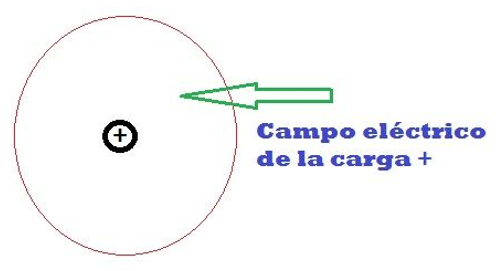
Fíjate en la figura, hemos puesto con un circulo la región del espacio donde si introducimos otra carga, se vería afectada por la carga eléctrica positiva de la figura. Esa región es lo que se llama el campo eléctrico de la carga +.

Cualquier carga que introduzcamos en el campo de la carga + se verá sometido a una fuerza debida al campo eléctrico de esta carga. Esta fuerza será mayor cuanto más cerca esta una carga de la otra, es decir depende de la posición dentro del campo eléctrico.
La dirección de esa fuerza a la que se va a ver sometida la carga que pongamos dentro del campo va a depender del tipo de carga que sea. ¿Te suena los polos contrarios se atraen? Pues bien, si las cargas son iguales la fuerza que tendrá hará que se repelan (se separen) y si son distintas, por ejemplo, una + y la otra -, la fuerza será tal que hará que se atraigan (se junten).

Conclusión : El tamaño de la fuerza depende de la posición dentro del campo, pero la dirección de la fuerza dependerá del tipo que sean, cargas iguales o diferentes. Recuerda que las fuerzas se representan por medio de vectores.



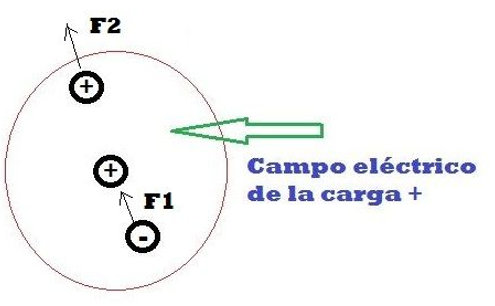
Si somos capaces de dejar quieta la carga que introducimos en el campo, esta no generará trabajo, pero si tendrá energía, ya que al soltarla se moverá por la acción de la fuerza a la que se ve sometida, igual que la piedra de la que hablamos al principio. En el caso de la piedra la fuerza era producida por la gravedad de la tierra. En el caso de una carga eléctrica la fuerza será producida por estar dentro de un campo eléctrico. Es por eso que la energía que tendrá la carga dentro del campo se llamará energía potencial y eléctrica, ya que es producida por el campo eléctrico.

Tienes que darte cuenta que al introducir una nueva carga dentro del campo de la +, la carga que introducimos nueva también tiene su propio campo, lo que hace que también sobre la carga + inicial, se genere una fuerza por causa del campo de la nueva carga que entra en su campo. Es decir 2 cargas tienen dos campos y si las dos cargas están dentro de cada uno de los campos producidos por cada una de ellas, las dos cargas tendrán una fuerza. Las dos cargas o se separan o se juntan.



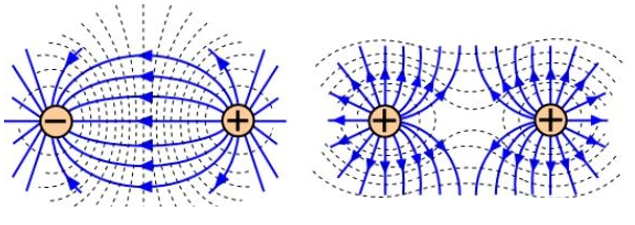
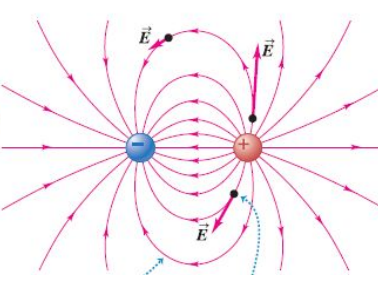
En la imagen de arriba hemos representado los dos casos posibles con las llamadas líneas de campo, que simplemente son unas líneas que representan las fuerzas dentro de los campos eléctricos. Son líneas imaginarias que describen, si los hubiere, los cambios en dirección de las fuerzas al pasar de un punto a otro dentro del campo.

Ley de Coulomb

Todas estas cantidades de fuerza y de energía se pueden calcular matemáticamente mediante una fórmula.
¿Con qué fuerza se atraen o repelen las cargas? Coulomb, físico e ingeniero francés, nos dio la solución con su ley. Aquí tienes la fórmula:

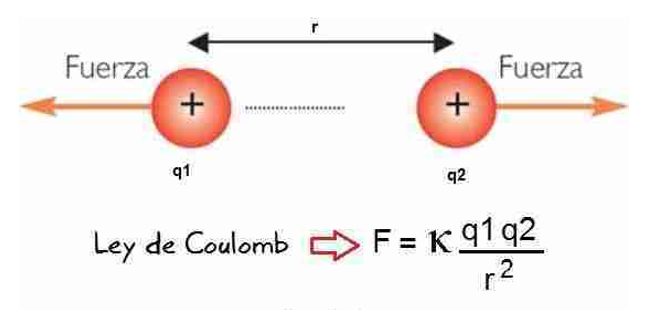
Dentro de la fórmula tenemos:
$F$ = Fuerza de atracción o repulsión medida en Newtons (N).

$K$ = Constante llamada constante de proporcionalidad o de coulomb que depende del medio en el que estén las cargas y de las unidades en las que se expresen el resto de elementos que hay dentro de la fórmula. Expresando todo en el Sistema Internacional de Unidades de Medida y en el vacío vale $9 \cdot 10^{9} \frac{N \cdot m^{2}}{C^{2}}$

$q_{1}$ = carga eléctrica de 1 expresada en Coulumbios ($C$).

$q_{2}$ = carga eléctrica de 2 expresada en Coulumbios ($C$).

$r$ = distancia que separa las dos cargas en metros ($m$).

Si te fijas bien, te darás cuenta que si incluyes el signo en los valores de las cargas, el valor de la fuerza eléctrica en esta expresión puede venir acompañada de un signo. Este signo será:

• Fuerza positiva. cuando la fuerza sea de repulsión\

• Fuerza negativa. cuando la fuerza sea de atracción.

La energía potencial eléctrica que posee una carga puntual q1 en presencia de otra carga puntual q2 que se encuentran separadas cierta distancia es:

$E_{p} = K \cdot \frac{q_{1} \cdot q_{2}}{r}$

• $E_{p}$ es la energía potencial eléctrica. En el S.I. se mide en Julios ($J$).


• $q_{1}$ y $q_{2}$ son los valores de las dos cargas puntuales. En el S.I. se miden en Coulombios ($C$).


• $r$ es el valor de la distancia que las separa. En el S.I. se mide en metros ($m$).
  
• $K$ es la constante de la ley de Coulomb. Para el vacío su valor es aproximadamente $9 \times 10^{9} \frac{N \cdot m^{2}}{C^{2}}$ utilizando unidades en el S.I.

Esta energía potencial será positiva si las cargas poseen el mismo signo y negativa si tienen signos distintos.

Recuerda esa energía potencial eléctrica será la capacidad que tendrá para realizar trabajo la carga eléctrica, en este caso para moverse cuando la soltemos dentro del campo eléctrico.

El trabajo que realiza una fuerza eléctrica para desplazar una carga desde un punto A hasta otro B puede expresarse de la siguiente forma:

$W_{e}(A \rightarrow B) = -(E_{pB} – E_{pA}) = E_{pA} – E_{pB}$

Si te fijas en la fórmula podríamos decir que el trabajo es igual al incremento de la energía potencial eléctrica. $W_{e}$, es el trabajo para desplazarse de $A$ hasta $B$.

Potencial Electrico

En electricidad, normalmente es mas conveniente usar la energía potencial eléctrica por unidad de carga, llamado expresamente potencial eléctrico. Es decir, la energía potencial, pero por cada unidad de carga, por cada coulomb.

Esta nueva magnitud, el potencial eléctrico se mide en voltios y su fórmula sería:

$U = \frac{E_{p}}{Q}$

$U$ = Potencial Eléctrico = $\frac{julios}{Coulumbios}$ = Voltios

$E_{p}$ = Energía Potencial en Julios.

$Q$ = Carga (Cantidad de Coulumbs de la carga) en $C$.

Podríamos definir el potencial eléctrico en un punto de un campo eléctrico como la energía potencial eléctrica que posee la unidad de carga positiva situada en ese punto.

Si en la fórmula de la energía potencial la carga que introducimos en el campo la ponemos el valor de 1C, tendremos la fórmula del potencial eléctrico:

$U = K \times (\frac{q}{r})$ siendo $q$ la carga que produce el campo.

Esto es muy útil, pues si tenemos un campo eléctrico podríamos definir el potencial eléctrico en cualquier punto del campo sin necesidad de saber de que valor será la carga que luego coloquemos allí.

Mira aquí definimos 3 puntos de potencial eléctrico en un campo: $V_{1}$, $V_{2}$ y $V_{3}$.

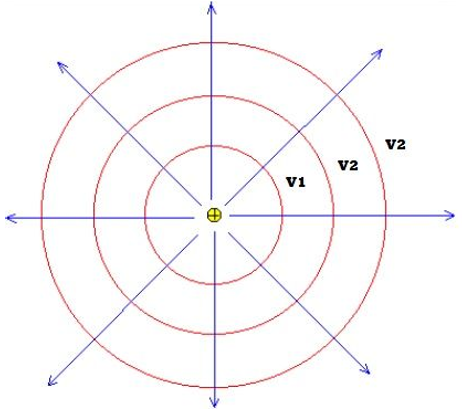
¿Por qué representarlo con un círculo? Porque la energía potencial eléctrica depende de la distancia, por lo tanto el potencial también, es la $E_{p}$ por unidad de carga. Todos los puntos que se encuentren a la misma distancia de la carga central tendrán el mismo potencial eléctrico.

Imagina que a la distancia del círculo $V_{1}$, todos eso puntos del círculo tienen un potencial eléctrico de $V_{1}= 6V$. Simplemente si quisiéramos saber cual sería la energía potencial de una carga, por ejemplo de $3C$ si lo situamos en ese punto dentro del campo, solo tendríamos que multiplicar el potencial en ese punto por el valor de la carga que pongamos en ese punto, es decir en nuestro caso $E_{p} = 6V \times 3C = 18 J$.

Podríamos calcular los potenciales en todos los puntos del campo, bueno en unos cuantos puntos, y de esa forma cuando queramos introducir una carga dentro del campo, calcular su energía potencial eléctrica en un punto u otro, sería muy sencillo.

Tensión o Voltaje

Otra magnitud muy usada en electricidad es la diferencia de potencial también llamada tensión o voltaje. Es simplemente la diferencia que habrá entre dos puntos con potenciales eléctricos diferentes. Imagina que un punto dentro de un campo eléctrico tiene un potencial eléctrico de $5V$ y en otro punto es de $3V$, pues la Tensión será de $5 - 3 = 2V$.

Cuando en una pila medimos la tensión entre los dos bornes de la pila (negativo y positivo), lo que estamos es midiendo la tensión entre estos dos puntos. Lo mismo pasa en un enchufe.

CALCULO DE POTENCIAL ELÉCTRICO

Para encontrar el potencial $V$ debido a una sola carga puntual $q$, se divide la energía potencial entre $q_{0}$:

$V = \frac{U}{q_{0}} = \frac{q}{4 \pi \epsilon_{0} r}$

Donde $r$ es la distancia de la carga puntual $q$ al punto en que se evalúa el potencial. Si $q$ es positiva, el potencial que produce es positivo en todos los puntos; si q es negativa, produce un potencial negativo en cualquier lugar.

El potencial debido a un conjunto de cargas puntuales (suma escalar):

$ V = \frac{U}{q_{0}} = \frac{1}{4 \pi \epsilon_{0} } \sum_i \frac{q_{i}}{r_{i}}$

(Potencial debido a un conjunto de cargas puntuales).

En una distribución contínua de carga a lo largo de una línea, superficie o volumen:

$V = \frac{1}{4 \pi \epsilon_{0}} \int \frac{dq}{r}$

(Potencial debido a una distribución continua de carga)

Donde $r$ es la distancia que hay entre el elemento con carga $dq$ y el punto del campo donde se desea obtener $V$.

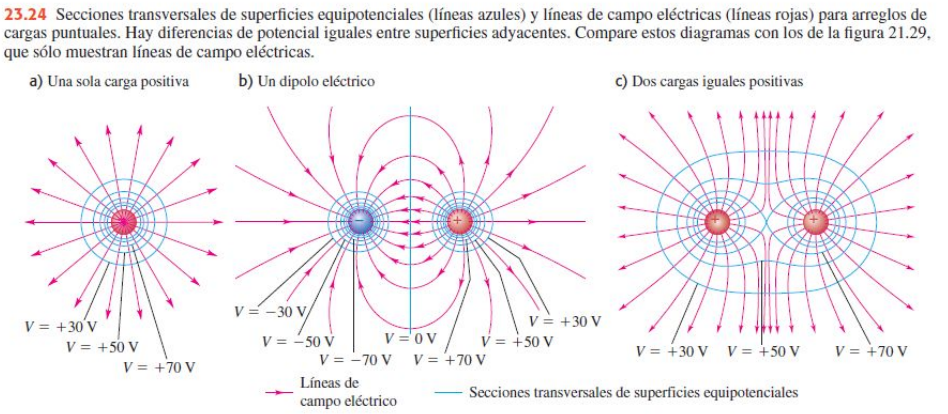
SUPERFICIE EQUIPOTENCIAL

Las líneas de campo nos ayudan a visualizar cómo es el comportamiento de distintas cargas que generan un campo eléctrico. El potencial en varios puntos de un campo eléctrico puede representarse gráficamente por medio de superficies equipotenciales. Se basan en el mismo concepto de un mapa topográfico, donde las curvas de nivel unen puntos que se encuentran a la misma elevación. Si una masa m se moviera sobre el terreno a lo largo de una curva de nivel, la energía potencial gravitacional $mgh$ no cambiaría porque la elevación h sería constante. Una superficie equipotencial es una superficie tridimensional sobre la que el potencial eléctrico V es el mismo en todos los puntos. Si una carga de prueba q0 se desplaza de un punto a otro sobre tal superficie, la energía potencial eléctrica q0V permanece constante. Las superficies equipotenciales para distintos potenciales nunca se tocan o intersecan.

La energía potencial no cambia a medida que una carga de prueba se traslada sobre una superficie equipotencial, por lo tanto el campo eléctrico no realiza trabajo sobre esa carga. Las líneas de campo y las superficies equipotenciales siempre son perpendiculares entre sí. Para un campo uniforme, en el que las líneas de campo son rectas, paralelas y están igualmente espaciadas, las superficies equipotenciales son planos paralelos perpendiculares a las líneas de campo.

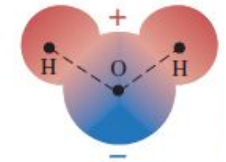
DIPOLO ELÉCTRICO

Un dipolo eléctrico consiste en un par de cargas puntuales de igual magnitud y signos opuestos (una carga positiva q y una carga negativa -q) separadas por una distancia d. Un ejemplo de un dipolo eléctrico es una molécula de agua, los enlaces químicos dentro de la molécula ocasionan un desplazamiento de la carga, formando así un dipolo. Cuando la sal se disuelve en agua, la sal se disocia en un ion de sodio positivo ($Na_{1}$) y un ion de cloro negativo ($Cl_{2}$), los cuales tienden a ser atraídos hacia los extremos negativo y positivo, respectivamente, de las moléculas de agua.

CAMPO EN UN DIPOLO ELÉCTRICO

Se refiere a un dipolo eléctrico como una fuente de campo eléctrico. En cada punto de la distribución, el campo total es la suma vectorial de los campos generados por dos cargas individuales. Para su cálculo se usa el principio de superposición de campos eléctricos para sumar las contribuciones de las cargas individuales al campo.