• Ir a
  • Introduccion
  • Contenidos
  • Videos
  • Informes
  • Quiero informacion

    • Corrientes Eléctricas Variables

    Capitulo 8

    Contenido: Inductancia, resistencia y capacidad en circuitos eléctricos, Circuitos RL, LC, RC, RLC, Potencia en circuitos de corriente alterna.

    Inductancia

    Interacción magnética entre dos alambres que transportan corrientes estables; la corriente en uno de los alambres genera un campo magnético que ejerce una fuerza sobre la corriente en el otro alambre. Pero cuando hay una corriente variable en uno de los circuitos, surge una interacción adicional. Considere dos bobinas de alambre cerca una de la otra, como se ilustra en la figura . Una corriente que circula por la bobina 1 produce un campo magnético y, por lo tanto, un flujo magnético a través de la bobina 2. Si la corriente en la bobina 1 cambia, el flujo a través de la bobina 2 también cambia; de acuerdo con la ley de Faraday, esto induce una fem en la bobina 2. De este modo, un cambio en la corriente de un circuito.

    puede inducir otra corriente en un segundo circuito.

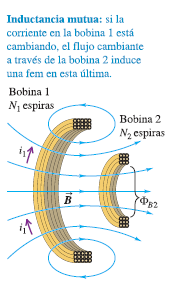
    En la figura, una corriente $i_{1}$ establece un campo magnético, y algunas de estas líneas de campo pasan a través de la bobina 2. Denotaremos con $\phi_{B2}$ el flujo magnético a través de cada espira de la bobina 2, causado por la corriente $i_{1}$ en la bobina 1. El campo magnético es proporcional a i1, de manera que B2 también es proporcional a $i_{1}$. Cuando $i_{1}$ cambia, $\phi_{B2}$ cambia; este flujo cambiante induce una fem $\epsilon_{2}$ en la bobina 2, dada por

    $\epsilon_{2}=\frac{-N_{2}d\Phi_{B2}}{dt}$

    Podríamos representar la proporcionalidad entre $\Phi_{B2}$ e $i_{1}$ en la forma $\Phi_{B2}=(constante)i_{1}$, pero, en vez de ello, es más conveniente incluir el número de espiras $N_{2}$ en la relación. Al introducir una constante de proporcionalidad $M_{21}$, llamada inductancia mutua de las dos bobinas, escribimos:

    $N_{2}d\Phi_{B2}=M_{21}i_{1}$

    donde B2 es el flujo a través de una sola espira de la bobina 2. De ahí que,

    $\frac{N_{2}d\Phi_{B2}}{dt}=M_{21}\frac{di_{1}}{dt}$

    Nos queda:

    $\epsilon_{2}=-M_{21}\frac{di_{1}}{dt}$

    También se podría escribir la definición de la inductancia mutua, como:

    $N_{2}d\Phi_{B2}i_{1}=M_{21}$

    $M_{21}$ siempre es igual a $M_{21}$, aun cuando las dos bobinas no sean simétricas. A este valor común lo llamamos simplemente inductancia mutua, y lo denotamos con el símbolo $M$, sin subíndices; este valor caracteriza por completo la interacción de la fem inducida de las dos bobinas. De esta forma, podemos escribir:

    $\epsilon _{2}=-M\frac{di_{1}}{dt} y \epsilon_{1}=-M\frac{di_{2}}{dt}$

    donde la inductancia mutua M es

    $M=\frac{N_{2}\Phi _{B2}}{i_{1}}=\frac{N_{1}\Phi_{B1}}{i_{2}}$

    La unidad del SI para la inductancia mutua se llama henry (1 H)

    Circuitos RL

    Un circuito que incluye tanto un resistor como un inductor, y tal vez una fuente de fem, se llama circuito R-L. El inductor ayuda a impedir los cambios rápidos en una corriente, lo que puede ser útil si se requiere una corriente estable y la fuente externa tiene una fem fluctuante. El resistor R puede ser un elemento de circuito individual, o ser la resistencia de los devanados el inductor. Al cerrar el interruptor S1 se conecta la combinación R-L a una fuente con fem constante E.

    Suponga que, en un principio, ambos interruptores están abiertos, y luego, en cierto momento inicial t=0 se cierra el interruptor S1. La corriente no puede cambiar súbitamente de cero a algún valor final porque di/dt y la fem inducida en el inductor serían infinitas. En vez de ello, la corriente comienza a crecer con una tasa que sólo depende del valor de L en el circuito. Sea i la corriente en cierto momento t después de que se cerró el interruptor S1, y sea di/dt su tasa de cambio en ese instante. La diferencia de potencial Vab a través del resistor en ese momento es: Vab=iR y la diferencia de potencial Vbc a través del inductor es Vbc=Ldidt

    Aplicamos la ley de mallas de Kirchhoff, comenzando en la terminal negativa y avanzando en sentido antihorario alrededor del circuito:

    $\epsilon -ir-L\frac{di}{dt}=0$

    Se despeja di/dt y se encuentra que la tasa de aumento de la corriente es

    $\frac{di}{dt}=\frac{(\epsilon -iR)}{L}$

    En el instante en que el interruptor S1 se cierra por primera vez, i=0 y la caída del potencial a través de R es igual a cero. La tasa de cambio inicial de la corriente es didt inicial=L. Cuando la corriente se acerca a un valor final I de estado estable. Cuando alcanza ese valor, su tasa de incremento es igual a cero. Entonces, didt final=0=ε-IRL=, I=R

    Expresión para la corriente como función del tiempo dii-R=-RLdt. Esto separa las variables, con i en el lado izquierdo y t en el derecho. Después se integran ambos lados, cambiando el nombre de las variables de integración a i’ y t’ y para utilizar i y t como límites superiores. Se obtiene:

    $\int_{0}^{i}{}\frac{di'}{(i'-\frac{\epsilon}{R})}=\int_{0}^{t}{}-\frac{R}{L}dt'$
    $\ln ?(\frac{i-\frac{\epsilon }{R}}{(-\frac{\epsilon}{R})})=-\frac{R}{L}t$

    A continuación, se aplica la función exponencial a ambos lados y se despeja i; el resultado final es:

    $i=\frac{\epsilon }{R}(1-e^{-\frac{R}{L}t}?)$

    Constante de tiempo del circuito:

    $\tau =\frac{L}{R}$

    Las consideraciones acerca de la energía brindan una perspectiva adicional sobre el comportamiento de un circuito R-L. La tasa instantánea con la que la fuente entrega energía al circuito es P= Ei . La tasa instantánea con que se disipa energía en el resistor es i2R, y la tasa con que se almacena energía en el inductor es iv bc =Li di/dt. Cuando se multiplica la ecuación, obtenida por la ley de mallas, por i y se reordena, se encuentra que:

    $\epsilon i=i^{2}R+Li\frac{di}{dt}$

    De la potencia Εi suministrada por la fuente, la parte (i2R) se disipa en el resistor, y la parte (Li di/dt) es la energía almacenada en el inductor.

    Circuitos RC

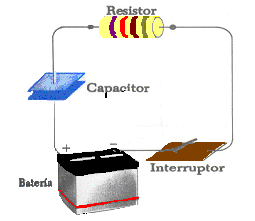
    Los circuitos RC son circuitos que están compuestos por una resistencia y un condensador. Se caracteriza por que la corriente puede variar con el tiempo. Cuando el tiempo es igual a cero, el condensador está descargado, en el momento que empieza a correr el tiempo, el condensador comienza a cargarse ya que hay una corriente en el circuito. Debido al espacio entre las placas del condensador, en el circuito no circula corriente, es por eso que se utiliza una resistencia. Cuando el condensador se carga completamente, la corriente en el circuito es igual a cero.

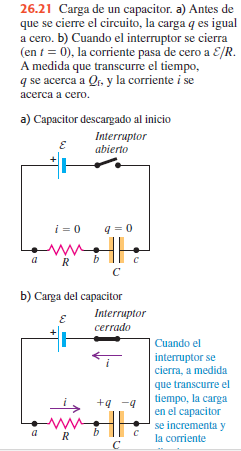
    Carga de un capacitor

    La figura muestra un circuito simple para cargar un capacitor. Un circuito como éste, que tiene un resistor y un capacitor conectados en serie, se llama circuito R-C. Se ha idealizado la batería (o fuente de energía eléctrica) para que tenga una fem ε constante y una resistencia eléctrica igual a cero (r=0), y se desprecia la resistencia de todos los conductores de conexión. Se comienza con el capacitor descargado (figura a); después, en cierto momento inicial, t = 0, se cierra el interruptor, lo que completa el circuito y permite que la corriente alrededor de la espira comience a cargar el capacitor (figura b). Para todos los efectos prácticos, la corriente comienza en el mismo instante en todas las partes conductoras del circuito, y en todo momento la corriente es la misma en todas ellas.

    Como el capacitor de la figura al principio está descargado, la diferencia de potencial vbc a través suyo es igual a cero en t = 0. En ese momento, según la regla de Kirchhoff de las espiras, el voltaje vab a través del resistor R es igual a la fem de la batería ε. La corriente inicial (t = 0) a través del resistor, que llamaremos I0, está dada por la ley de Ohm: I0 = vab/R= ε/R.

    A medida que el capacitor se carga, su voltaje vbc aumenta y la diferencia de potencial vab a través del resistor disminuye La suma de estos dos voltajes es constante e igual a ε. Después de un periodo largo, el capacitor está cargado por completo, la corriente baja a cero y la diferencia de potencial vab a través del resistor se vuelve cero. En ese momento aparece la totalidad de la fem ε de la batería a través del capacitor y vbc=ε.

    Sea q la carga en el capacitor e i la corriente en el circuito al cabo de cierto tiempo t después de haberse cerrado el interruptor. Asignamos el sentido positivo a la corriente en correspondencia al flujo de carga positiva hacia la placa izquierda del capacitor, como se aprecia en la figura b. Las diferencias de potencial instantáneas vab y vbc son

    $V_{ab}=iR V_{bc}=\frac{q}{C}$

    Con la regla de Kirchhoff de las espiras, se obtiene:

    $\epsilon -iR-\frac{q}{C}=0$

    El potencial cae en una cantidad iR conforme se va de a a b, y en q/C al pasar de b a c. Al despejar i en la ecuación, se encuentra que:

    $i=\frac{\epsilon }{R}-\frac{q}{RC}=0$

    En el momento $t = 0$, cuando el interruptor se encuentra cerrado, el capacitor está descargado y $q= 0$. Al sustituir $q= 0$ en la ecuación, se encuentra que la corriente inicial $I_{0}$ está dada por $I_{0} = \frac{\epsilon}{R}$, como ya se había dicho. Si el capacitor no estuviera en el circuito, el último término de la ecuación (26.10) no estaría presente, por lo que la corriente sería constante e igual a $\frac{\epsilon}{R}$. Conforme la carga se incrementa, el término $\frac{q}{RC}$ se hace más grande y la carga del capacitor tiende a su valor final, al que llamaremos $Qf$. La corriente disminuye y finalmente se vuelve cero. Cuando $i = 0$, la ecuación da:

    $\frac{\epsilon }{R}=\frac{Qf}{RC} Qf=C\epsilon $

    Es posible obtener expresiones generales para la carga q y la corriente i como funciones del tiempo

    $\frac{dq}{dt}=\frac{\epsilon}{R}-\frac{q}{RC}=-\frac{1}{RC}(q-C\epsilon )$
    $\frac{dq}{q-C\epsilon }=-\frac{dt}{RC} $

    luego se integran ambos lados. Podemos cambiar las variables de integración a q’ y t’ con la finalidad de utilizar q yt para los límites superiores. Los límites inferiores son q r = 0 y t r = 0:

    $\int_{0}^{q}{}\frac{dq'}{q-C\epsilon}=\int_{0}^{t}{}-\frac{dt'}{RC} $

    Se efectúa la integración y luego se aplica la función exponencial (es decir, se toma el logaritmo inverso) y se despeja q, para obtener:

    $q=C\epsilon(1-e^{-\frac{t}{RC}})=Qf(1-e^{-\frac{t}{RC}})$

    La corriente instantánea i tan sólo es la derivada con respecto al tiempo de la ecuación anterior:

    $i=\frac{dq}{dt}=\frac{\epsilon}{r}e^{-\frac{t}{RC}}=I_{0}e^{-\frac{t}{RC}}$

    Constante de tiempo del circuito:

    $\tau =RC$

    Descarga de un capacitor

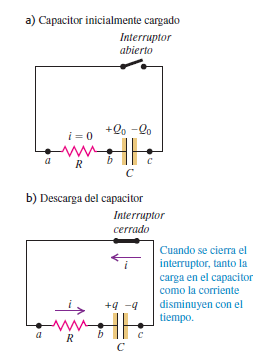
    Otra vez, i y q representan la corriente y la carga como función del tiempo en cierto instante después de que se hizo la conexión. En la figura b se hace la misma selección del sentido positivo para la corriente que en la figura b anterior. Entonces, la regla de Kirchhoff de las espiras da la ecuación, pero con $V = 0$; es decir,

    $i=\frac{dq}{dt}=-\frac{q}{RC}$
    Carga: $q=Q_{0}e^{-\frac{t}{RC}}$

    Corriente instantánea:

    $i=\frac{dq}{dt}=-\frac{Q_{0}}{RC}e^{-frac{t}{RC}}=I_{0}e^{\frac{t}{RC}}$

    Potencia:

    $\epsilon i=i^{2}R+\frac{iq}{C}$

    Circuito LC

    Un circuito que contiene un inductor y un capacitor muestra un modo completamente nuevo de comportamiento, caracterizado por una corriente y una carga oscilantes. Esto está en claro contraste con el enfoque exponencial de la situación de estado estable que hemos visto para circuitos tanto R-C como R-L. En el circuito L-C de la figura se carga el capacitor con una diferencia de potencial Vm y una carga inicial $Q = C \cdot V \cdot m$ en su placa izquierda y luego se cierra el interruptor.

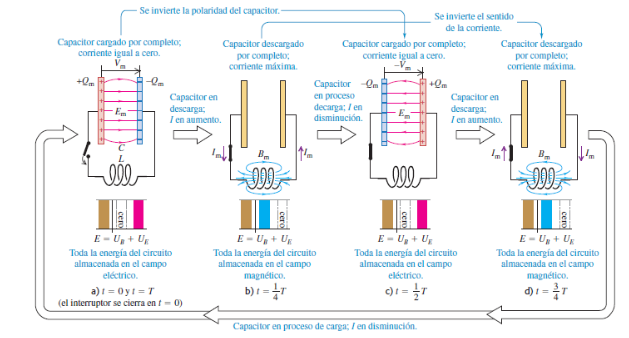
    El capacitor comienza a descargar a través del inductor. A causa de la fem inducida en el inductor, la corriente no puede cambiar en forma instantánea; comienza en cero y finalmente alcanza un valor máximo $I \cdot m$. Durante esta intensificación el capacitor se está descargando. En cada instante el potencial del capacitor es igual a la fem inducida, por lo que a medida que el capacitor se descarga, la tasa de cambio de la corriente disminuye. Cuando el potencial del capacitor se reduce a cero, la fem inducida también es igual a cero, y la corriente se ha estabilizado en su valor máximo $I \cdot m$. La diferencia de potencial entre sus terminales (y las del inductor) ha disminuido hasta cero, y la corriente alcanzó su valor máximo $I \cdot m$.

    La diferencia de potencial entre sus terminales (y las del inductor) ha disminuido hasta cero, y la corriente alcanzó su valor máximo $I \cdot m$. Aunque en la figura b el capacitor está completamente descargado, la corriente persiste y el capacitor comienza a cargarse con polaridad opuesta a la de su estado inicial. Conforme disminuye la corriente, la magnitud del campo magnético también lo hace, lo que induce una fem en el inductor en el mismo sentido que el de la corriente; esto retarda la disminución de la corriente. Con el tiempo, la corriente y el campo magnético disminuyen a cero y el capacitor queda cargado en el sentido opuesto al de su polaridad inicial (figura c), con una diferencia de potencial $2 \cdot V \cdot m$ y carga $2 \cdot Q$ en su placa izquierda.

    El proceso se repite ahora en sentido opuesto; un poco después, el capacitor se ha descargado una vez más y en el inductor hay una corriente en el sentido opuesto (figura d). Más tarde, la carga del capacitor recupera su valor original (figura a), y todo el proceso se repite. Si no hay pérdidas de energía, las cargas en el capacitor siguen oscilando hacia atrás y adelante indefinidamente. Este proceso se llama oscilación eléctrica.

    Oscilaciones eléctricas en un circuito LC

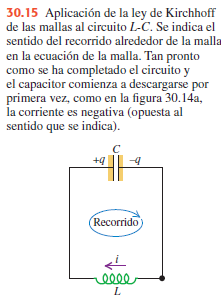
    Se aplica la ley de Kirchhoff de las mallas al circuito de la figura. Partiendo de la esquina inferior derecha del circuito y sumando los voltajes conforme se recorre la espira en el sentido horario, se obtiene lo siguiente:

    $-L\frac{di}{dt}-\frac{q}{c}=0$

    Como $ i = \frac{dq}{dt}$, se deduce que $\frac{di}{dt} =\frac{d^{2}q}{dt^{2}}$. Sustituimos esta expresión en la ecuación anterior y se divide entre $-L$ para obtener

    $\frac{d^{2}q}{dt^{2}}+\frac{1}{LC}q=0$

    La carga q del capacitor está dada por: $q=Q \cdot cos( \omega t+\phi)$ y la frecuencia angular de la oscilación está dada por $\omega=1LC$. Al hacer esto, encontrará que la corriente instantánea $i = \frac{dq}{dt}$ está dada por: $ i = -\omega t Q sen( \omega \cdot t + \phi )$

    Energía en un circuito L-C

    También se puede analizar el circuito L-C desde la perspectiva de la energía. El circuito L-C también es un sistema conservativo. Otra vez, sea Q la carga máxima del capacitor. La energía del campo magnético, $\frac{1}{2}Li^{2}$, en el inductor en cualquier momento corresponde a la energía cinética $\frac{1}{2}mv^{2}$ del cuerpo oscilante, y la energía del campo eléctrico $\frac{q_{2}}{2 \cdot C}$ en el capacitor corresponde a la energía potencial elástica del resorte. La suma de estas energías es igual a la energía total $\frac{Q_{2}}{2 \cdot C}$Q del sistema:

    $\frac{1}{2}Li^{2}+\frac{q^{2}}{2C}=\frac{Q^{2}}{2C}$

    La energía total en el circuito L-C es constante; oscila entre las formas magnética y eléctrica, del mismo modo que la energía mecánica total en el movimiento armónico simple es constante y oscila entre las formas cinética y potencial. Al despejar i en la ecuación anterior se encuentra que cuando la carga en el capacitor es q, la corriente i es:

    $i=\pm \sqrt{\frac{1}{LC}}\sqrt{Q^{2}-q^{2}}$

    Circuito RCL

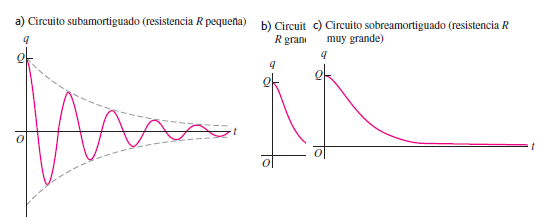
    Suponga que un inductor con inductancia L y un resistor de resistencia R están conectados en serie entre las terminales de un capacitor cargado, para formar un circuito en serie L-R-C. Como antes, el capacitor comienza a descargarse tan pronto como el circuito está completo. Si la resistencia R es relativamente pequeña, el circuito aún oscila, pero con un movimiento armónico amortiguado (figura), y se dice que el circuito está subamortiguado. Si R se incrementa, las oscilaciones cesan con más rapidez. Cuando R alcanza cierto valor, el circuito deja de oscilar; está críticamente amortiguado (figura b). Para valores aún mayores de R, el circuito está sobreamortiguado (figura c), y la carga del capacitor se acerca a cero aún más lentamente.

    Análisis Circuito LRC

    Para analizar con detalle el comportamiento del circuito L-R-C, consideremos el circuito que aparece en la figura 30.17. Las indicaciones de los sentidos positivo de q e i son las mismas que para el circuito L-C.

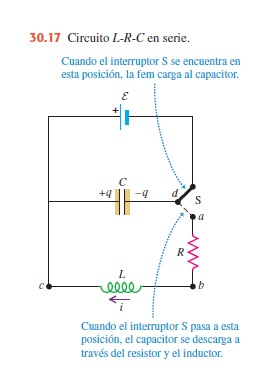
    Primero se cierra el interruptor en la posición hacia arriba, para conectar al capacitor con una fuente de fem ε durante un tiempo suficientemente largo para asegurar que el capacitor adquiera su carga final $\textit{Q }=\textit{C}_{\epsilon}$ que toda oscilación inicial haya cesado. Entonces, en el momento $t = 0$ se coloca al interruptor en la posición hacia abajo, con lo que se elimina a la fuente del circuito y se pone al capacitor en serie con el resistor y el inductor. Note que la corriente inicial es negativa y con sentido opuesto al de i que se ilustra en la figura.

    se aplica la ley de Kirchhoff de las mallas. Partiendo del punto a y recorriendo el circuito en el sentido abcda, se obtiene la ecuación:

    $$-iR-L\frac{di}{dt}-\frac{q}{C}=0$$

    Al sustituir $\textit{i }$ con $\textit{dq}/\textit{dt}$ y reordenar, se obtiene:

    $\frac{d^{2}q}{dt^{2}}+\frac{R}{L}\frac{dq}{dt}+\frac{1}{LC}q=0$

    Hay métodos generales para obtener soluciones de la ecuación anterior. La forma de la solución es diferente para los casos del circuito sub amortiguado (R pequeña) y sobre amortiguado (R grande). Cuando R2 es menor que 4L/C, la solución tiene la forma

    $q=Ae^{-(\frac{R}{2L})t}\cos?(\sqrt{\frac{1}{LC}-\frac{R^{2}}{4L^{2}}t}+\varphi )$

    donde A y son constantes.

    La frecuencia angular de las oscilaciones amortiguadas está dada por

    $\omega ^{'}=\sqrt{\frac{1}{LC}-\frac{R^{2}}{4L^{2}}}$

    Potencia en Corriente Alterna

    En corriente alterna existen desfasajes entre la tensión y la corriente debido a las capacidades e inductancias del circuito que crean campos eléctricos y magnéticos.


    La energía que almacenan temporalmente estos campos se devuelve al circuito (por ejemplo, cuando el capacitor se descarga o el campo magnético del inductor se autoinduce). Esto hace que la potencia total suministrada por la fuente no siempre sea la consumida por el circuito. Una parte de la potencia se utiliza para crear esos campos, pero no se consume. Sin embargo, la fuente debe proveerla para el funcionamiento del circuito.

    Potencia activa, reactiva y aparente

    Encontramos en este tipo de circuito tres valores distintos de potencia, denominados potencia activa, potencia reactiva y potencia aparente.

    Potencia activa (P)

    Es la potencia consumida en el circuito (por ejemplo, convertida en calor, energía mecánica, etc.). Se mide en watt.

    $P=I_{EF}^{2}\cdot R$

    Potencia reactiva (Q)

    Es la potencia necesaria para crear los campos eléctricos y magnéticos. Es una potencia devuelta por el circuito, pero que está presente en el funcionamiento. Se mide en VAR (volt ampere reactivos), una unidad equivalente al watt.

    $Q=I_{EF}^{2}\cdot (X_{L}-X_{C})$

    Potencia aparente (S)

    Es la suma (en forma vectorial) de las potencias activa y reactiva. Su valor depende del ángulo de desfasaje. Es la potencia total que debe entregar el generador. Se mide en VA (volt ampere), una unidad equivalente al watt.

    $S=I_{EF}^{2}\cdot Z$

    Triángulo de potencia

    Podemos representar a las tres potencias en un triángulo rectángulo en donde el cateto horizontal es la potencia activa, el cateto vertical es la potencia reactiva y la hipotenusa es la potencia aparente.

    El siguiente ejemplo es un triángulo de potencias para un circuito inductivo ya que la potencia reactiva es positiva.

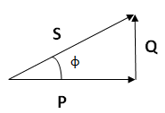
    El siguiente ejemplo es un triángulo de potencias para un circuito inductivo con menor potencia reactiva que el ejemplo anterior.

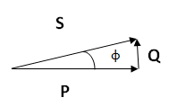
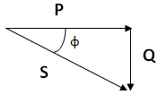
    El siguiente triángulo corresponde a un circuito capacitivo ya que la potencia reactiva es negativa.



    Capitulo 8

    Temas Tratados.

    • Inductancia.
    • Resistencia y capacidad en circuitos eléctricos.
    • Circuitos RL, LC, RC, RLC.
    • Potencia en circuitos de corriente alterna.