Fuerzas Magnéticas y Campos Magnéticos
Capitulo 6
Contenido: Polos magnéticos y líneas de campo magnético, Fuerza magnética sobre cargas en movimiento, Campo magnético, Fuerza y torque sobre corrientes en un campo magnético. Momento magnético, Ley de Biot-Savart, Distribuciones de corriente, Ley de Ampere, Dipolos magnéticos y sus aplicaciones
Introduccion
La naturaleza fundamental del magnetismo es la interacción de las cargas eléctricas en movimiento. Las fuerzas eléctricas, que actúan sobre las cargas eléctricas, tienen este comportamiento independientemente si están en movimiento o no, Las fuerzas magnéticas sólo actúan sobre cargas que se mueven.
Las fuerzas eléctricas ocurren en dos etapas: primero una carga produce un campo eléctrico en el espacio que la rodea y una segunda carga responde a este campo. Las fuerzas magnéticas también ocurren en dos etapas. En primer lugar, una carga o conjunto de cargas en movimiento (es decir, una corriente eléctrica) producen un campo magnético. A continuación, una segunda corriente o carga en movimiento responde a ese campo magnético, con lo que experimenta una fuerza magnética.
Magnetismo
Los imanes permanentes ejercen fuerza uno sobre otro y sobre trozos de hierro que no estaban magnetizados. Cuando una varilla de hierro entraba en contacto con un imán natural, aquélla también se magnetizaba, y si la varilla flotaba en agua o se suspendía de un hilo por su parte central, tendía a alinearse con la dirección norte-sur. La aguja de una brújula ordinaria no es más que un trozo de hierro magnetizado.
Si un imán permanente en forma de barra tiene libertad para girar, uno de sus extremos señalará al norte. Este extremo se llama polo norte o polo N; el otro extremo es el polo sur o polo S. Los polos opuestos se atraen y los polos iguales se rechazan.
La Tierra misma es un imán. Su polo norte geográfico está cerca del polo sur magnético, lo cual es la razón por la que el polo norte de la aguja de una brújula señala al norte terrestre.
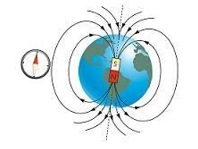
Esquema del campo magnético terrestre. Las líneas, llamadas líneas de campo magnético, muestran la dirección que señalaría una brújula que estuviera en cada sitio. La dirección del campo en cualquier punto se define como la dirección de la fuerza que el campo ejercería sobre un polo norte magnético.
Polos magnéticos contra carga eléctrica
La analogía entre polos magnéticos y carga eléctrica (polos norte y sur - cargas positiva y negativa) puede ser errónea. Los polos siempre ocurren por pares. Si un imán de barra se parte en dos, cada extremo se convierte en un polo.
Ahora sabemos que las fuerzas magnéticas entre dos cuerpos se deben fundamentalmente a interacciones entre los electrones en movimiento en los átomos de los cuerpos. En el interior de un cuerpo magnetizado, como un imán permanente, hay un movimiento coordinado de algunos electrones atómicos; en un cuerpo no magnetizado los movimientos no están coordinados.
Campo Magnético
Una carga o corriente móvil crea un campo magnético en el espacio circundante. El campo magnético ejerce una fuerza $\vec{F}$ sobre cualquier otra carga o corriente en movimiento presente en el campo.
El campo magnético es un campo vectorial, representado por $\vec{B}$. En cualquier posición, la dirección de $\vec{B}$ se define como aquella en la que tiende apuntar hacia fuera de su polo norte y hacia adentro de su polo sur.
Fuerzas magnéticas sobre cargas móviles
La fuerza magnética ejercida sobre una carga en movimiento tiene cuatro características esenciales.
- La magnitud es proporcional a la magnitud de la carga.
- La magnitud de la fuerza también es proporcional a la magnitud, o “intensidad”, del campo.
- La fuerza magnética depende de la velocidad de la partícula.
- La fuerza Magnética $\vec{F}$ no tiene la misma dirección que el campo magnético $\vec{B}$, sino que siempre es perpendicular tanto como a $\vec{B}$ como a la velocidad $\vec{v}$.
La magnitud de $\vec{F}$ esta dada por: $F=|Q|vBsin(ϕ)$ donde $|q|$ es la magnitud de carga y $ϕ$ es el ángulo medido desde la dirección de $\vec{v}$ hacia la dirección de $\vec{B}$.
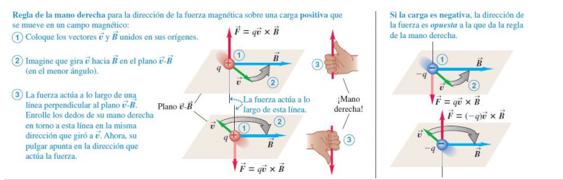
Para completar esta descripción se utiliza la ley de la mano derecha. Fuerza magnética sobre una partícula con carga en movimiento:
Válido tanto como para cargas positivas como negativas (evaluar de forma correcta el sentido de la fuerza dada por una carga positiva o negativa - ley de la mano derecha). Si dos cargas con magnitud igual y signos contrarios se mueven con la misma velocidad en el mismo campo $\vec{B}$, las fuerzas tienen igual magnitud y dirección opuesta. La ecuación de la magnitud de la fuerza magnética $\vec{F}$:
Hay veces en que esta forma es más conveniente, en especial en problemas que incluyen corrientes en vez de partículas individuales. La unidad de SI para $B$ es equivalente a $1 \frac{N \cdot s}{C}$. Ya que un ampere es un Coulomb por segundo ($1A =1 \frac{C}{s}$), $1 \frac{N \cdot m}{A}$. Esta unidad recibe el nombre de tesla ($T$).
Líneas de campo magnético y flujo magnético
Cualquier campo magnético se representa usando líneas de campo magnético, del mismo modo que hicimos para el campo magnético terrestre. Se dibujan las líneas de modo que la línea que pasa a través de cualquier punto sea tangente al vector del campo magnético en ese punto. Las líneas de campo nunca se cruzan.

Como los patrones de campo magnético son tridimensionales, con frecuencia es necesario dibujar líneas de campo magnético que apunten hacia dentro o hacia fuera del plano de un dibujo. Para hacer esto se usa un punto (.) que representa un vector dirigido hacia fuera del plano, y una cruz (x) que denota que el vector se dirige hacia el plano.
Fuerza y par de torsión en una espira de corriente
La espira se puede representar como una serie de segmentos rectilíneos. La fuerza total sobre la espira es igual a cero, pero puede haber un par de torsión neto que actúe sobre la espira, con algunas propiedades interesantes.
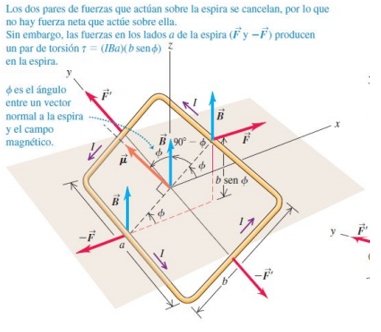
Sobre el lado opuesto de la espira actúa una fuerza $\vec{-F}$ con la misma magnitud, pero dirección opuesta. los lados con longitud $b$ forman un ángulo $(90°-ϕ)$ con la dirección de $\vec{B}$. Las fuerzas sobre estos lados son los vectores $\vec{F}$ y $\vec{-F^{'}}$; su magnitud $\vec{F^{'}}$ esta dada por:
La fuerza neta sobre una espira de corriente en un campo magnético uniforme es igual a cero. Sin embargo, el par de torsión neto en general no es igual a cero. El brazo de momento para cada una de estas fuerzas (igual a la distancia perpendicular desde el eje de rotación hasta la línea de acción de la fuerza) es ($\frac{b}{2}) sen(Φ)$, así que el par de torsión debido a cada fuerza tiene magnitud $F(\frac{b}{2}) sen Φ$.
La magnitud del par de torsión neto es $Τ=2F(\frac{b}{2})sen(ϕ)=(IBa)(bsen(ϕ))$. El par de torsión es máximo cuando Φ=90°, B está en el plano de la espira y la normal a este plano es perpendicular a $B$; El par de torsión es igual a cero cuando $Φ= 0°$ o $180°$ El área A de la espira es igual a ab, por lo que el torque neto se puede reescribir como: $Τ=I \cdot B \cdot A \cdot sen(ϕ)$. El producto IA se denomina momento dipolar magnético $\mu = I \cdot A$. En términos de $\mu$ la magnitud del par de torsión sobre una espira de corriente es $Τ=\mu \cdot B \cdot sen(ϕ)$, donde $ϕ$ es el ángulo entre la normal a la espira y $B$.
Ley de Biot-Savart
El campo magnético generado por varias cargas en movimiento es la suma vectorial de los campos generados por las cargas individuales. Comenzamos con el cálculo del campo magnético ocasionado por un segmento corto dl de un conductor que transporta corriente.
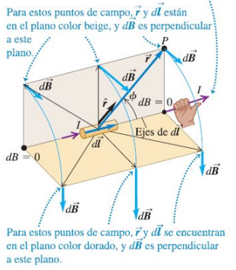
El volumen del segmento es $A \cdot dl$, donde $A$ es el área de la sección transversal del conductor. Si hay $n$ partículas con carga en movimiento por unidad de volumen, cada una con una carga $q$, de la carga total dQ que se mueve en el segmento es:
Las cargas en movimiento en este segmento son equivalentes a una sola carga $d \cdot Q$ que viaja con una velocidad igual a la velocidad de deriva $V \cdot \vec{d}$. La magnitud del campo resultante $d \vec{B}$ en cualquier punto $P$.
Por lo tanto,
En forma vectorial, usando el vector unitario, se tiene: $d\vec{B} = \frac{\mu_{0}}{4 \phi} \frac{I \cdot \vec{dl} \times \hat{r}}{r^{2}}$ donde $\vec{dl}$ es un vector con longitud $dl$, en la misma dirección que la corriente en el conductor. Esta ecuación constituye la ley de Biot y Savart. Esta ley se utiliza para encontrar el campo magnético total debido a la corriente en un circuito completo en cualquier punto en el espacio. Para hacerlo, se integra la ecuación con respecto a todos los segmentos que conduzcan corriente; en forma simbólica,
Existe una ley que nos permite obtener con más facilidad los campos magnéticos generados por distribuciones de corriente con un alto grado de simetría, llamada ley de Ampere, que es de carácter muy diferente del que tiene la ley de Gauss.
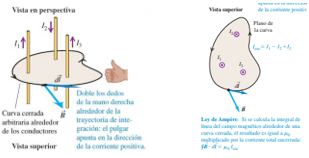
La ley de Ampere está formulada no en términos del flujo magnético, sino de la integral de línea de alrededor de una trayectoria cerrada que se denota como
Para evaluar esta integral, se divide la trayectoria en segmentos infinitesimales $\vec{dl} $ para cada uno de los cuales se calcula el producto escalar $\vec{B} \cdot \vec{dl}$, y se suman los resultados. En general, $\vec{B}$ varía de un punto al otro, y se debe emplear el valor de $\vec{B}$ en la ubicación de cada $\vec{dl}$. El círculo sobre el signo de la integral indica que ésta se calcula siempre para una trayectoria cerrada, es decir, una trayectoria cuyos puntos inicial y final son iguales.
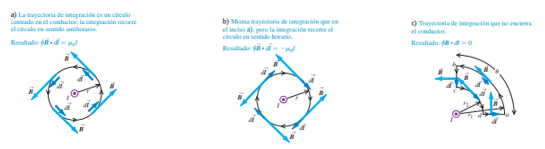
Para generalizar la Ley de Ampere, se supone que varios conductores largos y rectos pasan a través de la superficie limitada por la trayectoria de integración. Si la trayectoria de integración no encierra un alambre particular, la integral de línea del campo de ese alambre es igual a cero. Todo conductor presente que no esté encerrado por una trayectoria particular las integrales de línea de sus campos alrededor de la trayectoria tienen un valor de cero.
De esta forma, se puede reemplazar $I$ por $I_{enc}$, la suma algebraica de las corrientes encerradas o enlazadas por la trayectoria de integración, con la suma evaluada con base en la regla de los signos que se describe en la figura. Así, el enunciado de la ley de Ampere es
Energía Potencial para un Dipolo Magnético
Si un dipolo magnético cambia de orientación en un campo magnético, éste realiza trabajo sobre el campo, en un desplazamiento angular infinitesimal hay un cambio considerable en la energía potencial y esta energía es mínima $\vec{\mu}$ y $\vec{B}$ si son paralelos y es máxima cuando son antiparalelos.
El par de torsión sobre un dipolo eléctrico en un campo eléctrico es: $\vec{T} = \vec{p} \times \vec{E}$. El par de torsión sobre un dipolo magnético en un campo magnético es $\vec{T} = \vec{\mu} \times \vec{E}$.
La energía potencial es: $U = -\vec{\mu} \cdot \vec{B}$ donde $U=0$ cuando el momento dipolar magnético es perpendicular al campo magnético.
Dipolo Magnético en un Campo Magnético no Uniforme
Una espira de corriente experimenta una fuerza neta de cero en un campo magnético uniforme.
- Para la fuerza neta, las componentes radiales se cancelan.
- La fuerza neta es hacia la derecha, alejándose del imán.
Dipolo Magnético y cómo funcionan los Imanes
Al pensar en un electrón como en una esfera de carga giratoria, la circulación de carga en torno al eje de rotación es como una espira de corriente y, por ello, el electrón tiene un momento magnético neto. En un átomo de hierro, una fracción importante de los momentos magnéticos de los electrones se alinean entre sí, y el átomo tiene un momento magnético distinto de cero.
En un trozo de hierro no magnetizado no hay una alineación general de los momentos magnéticos de los átomos; su suma vectorial es cero, y el momento magnético neto también es cero, en un imán de barra, los momentos magnéticos de muchos de sus átomos son paralelos, y existe un momento magnético neto μ apreciable, si el imán se coloca en un campo magnético el campo ejerce un par de torsión dado por la ecuación que tiende a alinear $\mu$ con $B$.
Un imán atrae un objeto de hierro no magnetizado, se trata de un proceso en dos etapas:
- Los momentos magnéticos atómicos del hierro tienden a alinearse con el campo del imán, por lo que el hierro adquiere un momento dipolar magnético neto $\mu$ paralelo al campo.
- El campo no uniforme del imán atrae al dipolo magnético.
Capitulo 6
Temas Tratados.
- Polos magnéticos y líneas de campo magnético.
- Fuerza magnética sobre cargas en movimiento.
- Campo magnético.
- Fuerza y torque sobre corrientes en un campo magnético.
- Momento magnético.
- Ley de Biot-Savart.
- Distribuciones de corriente.
- Ley de Ampere.
- Dipolos magnéticos y sus aplicaciones.